A equação de Torricelli é a seguinte:
V2 = V02 + 2.a.∆S
Evangelista Torricelli (1608 – 1647)
Provavelmente mais conhecido por nós pela sua famosa equação que tanto utilizamos na física, mas deu importantes contribuições para a área como o barômetro, aperfeiçoou o telescópio, na matemática enunciou o teorema que determina o centro de gravidade de uma figura geométrica através de integrais.
Deduzindo a equação de Torricelli
A equação de Torricelli na qual iremos comentar pode ser facilmente deduzida por duas equações às quais são: a equação horário do espaço e o da velocidade, ambas do movimento uniformemente variado.
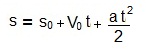
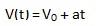
A equação de Torricelli que é v2= v02+2a∆s, não depende do tempo. Então a idéia e pegarmos uma das equações são tirarmos o valor de t e substituirmos a outra equação, assim não teremos mais a incógnita t. Observe que a melhor equação e mais prática para tirarmos o valor de t é a equação da velocidade, façamos assim:
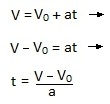
Agora esse valor de t vamos substituir na equação horária do espaço, ou seja, onde houver a letra t substituiremos pela expressão (v-v0)/a. Vamos lá? Colocarei esta expressão de t com outra cor para que possamos visualizar a substituição.
Agora iremos desenvolver a expressão:

Para facilitar nossa conta, vamos multiplicar todos os termos por 2:

Assim obtivemos equação de Torricelli.
E a velocidade, qual sinal usar na equação de Torricelli?
Há um detalhe que devemos discutir sobre o resultado da velocidade. Como a velocidade está ao quadrado, podemos ter duas respostas satisfatórias, ou seja:
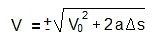
Qual sinal usar? Isto dependerá do sentido da trajetória, pois o sinal indica qual o sentido do movimento do objeto. Observe a ilustração:

Caso o objeto esteja se movendo no sentido positivo da trajetória (situação A), temos a velocidade com sinal positivo e movendo – se no sentido contrário da trajetória (situação B) temos o sinal contrário.
Texto enviado pelo Professor Adriando Marden de Souza Bastos.


valeu me ajudou muito
adorei o texto, muito obrigada, bom trabalho pra voces