Plano Inclinado com atrito

Vamos continuar estudando o plano inclinado, mas agora iremos avançar um pouco mais estudando o plano inclinado com atrito.

O plano inclinado foi uma invenção muito eficiente dos povos antigos, pois possibilitava elevar objetos pesados aplicando forças reduzidas. Um dos exemplos mais antigos da utilização das propriedades benéficas do plano inclinado é o caso das extensas rampas, pelas quais os egípcios movimentavam as pesadas pedras que constituem as maravilhosas pirâmides.

Cabe ressaltar que a energia necessária para se elevar um objeto, seja elevando-o diretamente ou por intermédio de um plano inclinado, é a mesma na ausência de efeitos dissipativos de energia (como atrito ou resistência do ar). Pela equação abaixo podemos ver que o trabalho (T) envolvido vale:

T= F x d equação 1

onde:

F = Força aplicada

d = Distância percorrida

O plano inclinado tem o efeito de reduzir a força aplicada necessária para se mover objetos, para isto usando uma distância maior, e mantendo o mesmo trabalho executado. Como exemplo do quão útil é este efeito, imagine que se queira projetar uma máquina para elevar cargas. Através de um plano inclinado esta máquina vai suportar cargas menores do que se tivessem que trabalhar erguendo essas mesmas cargas diretamente. Assim, a máquina que operar no plano inclinado poderá ser bem mais barata e até ter uma vida útil maior.

Vamos agora estudar um diagrama de um plano inclinado com atrito para ver o que acontece com as forças:

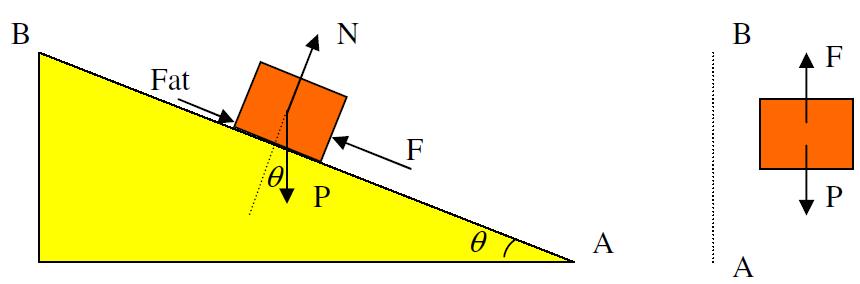
No gráfico da direita percebemos que para se elevar o objeto, a força F aplicada deve ser maior ou igual ao peso do objeto (F>=mg ). Já no plano temos que a força necessária para elevar o objeto é:

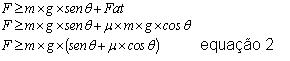
Reparem que no caso de não haver atrito (u=0 ), a mínima força F necessária para se elevar o objeto pelo plano inclinado vale: F = m x g x senθ. Esta força é portanto menor, por um fator senθ , do que a necessária se fosse feita uma elevação direta do objeto. Assim, podemos ver a utilidade do plano inclinado que tornou possível se aplicar uma força reduzida para se mover o mesmo objeto.

Contudo, analisando a equação 2, percebemos que se o fator entre parênteses for maior que 1, então, a força necessária para se elevar o objeto pelo plano inclinado será maior do que fosse feita por uma elevação direta. Isto ocorre quando:

Ou seja, se o coeficiente de atrito for superior a 0,577 para uma inclinação de 30 graus, será mais fácil elevar o objeto diretamente do que arrastá-lo por um plano inclinado.

Uma outra aplicação interessante de plano inclinado com atrito é a de um carro descendo uma ladeira e freando bruscamente (travando as rodas).

Neste exemplo, desde o instante em que o carro freia até ele parar, o carro está sujeito a uma força resultante que é a própria força de atrito contrária ao movimento de descida do carro. Podemos então escrever:

Do jeito como esta equação está montada, o sentido da força de atrito é positivo (ou seja, subindo a ladeira é positivo e descendo a ladeira é negativo). Desenvolvendo a equação:

Cortando as massas e rearrumando:

Dependendo do sinal do fator entre parênteses a aceleração do carro pode ser positiva (no sentido de frear) ou negativa (no sentido de acelerar). Pode parecer estranho, mas esta análise mostra que dependendo da conjunção entre os fatores de coeficiente de atrito e ângulo de inclinação, ao se frear o carro bruscamente você pode piorar ainda mais a situação, pois irá acelerar ao invés de frear. Este efeito prejudicial ocorre quando o fator entre parênteses é negativo.

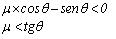
Por exemplo, suponha que você está de carro descendo uma ladeira. Se a inclinação da pista for de 15 graus e o coeficiente de atrito da pista for inferior a tg15 = 0,268 então tome muito cuidado. Não freie bruscamente jamais!!!